Midpoint Polygon Conjecture is false

Contrary to my expectations, my previous post turned out to be like  Popular-­Lonely primes and Decimal Problem, i.e. I discovered nothing new.

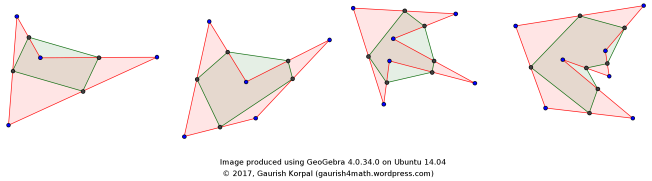
My conjecture is false. Following counterexample is given on pp. 234 of this paper:

Counterexample of the conjecture, taken from: Berlekamp, E. R., E. N. Gilbert, and F. W. Sinden. “A Polygon Problem.” The American Mathematical Monthly 72, no. 3 (1965): 233-41. doi:10.2307/2313689.

As pointed out by uncombed_coconut, the correct theorem is:

Theorem (Berlekamp-Gilbert-Sinden, 1965). For almost all simple polygons there exist a smallest natural number such that after iterations of midpoint polygon procedure, we obtain a convex polygon.

The proof of this theorem is very interesting. Till now I thought that proving euclidean geometry theorems using complex numbers was an overkill. But using an N-tuple of complex numbers to represent the vertices of a closed polygon (in given order),  ,  we can restate the problem in terms of eigenvectors (referred to as eigenpolygons) and eigenvalues.  Following are the crucial facts used is the proof:

• An arbitrary N-gon (need not be simple) can be written as a sum of regular N-gons i.e. the eigenvalues are distinct.
• The coefficient of eigenvector (when N-gon is written as linear combination of eigenpolygons) is the centroid of the polygon obtained by “winding” times.
• All vertices of the midpoint polygons (obtained by repeating the midpoint polygon procedure infinitely many times) converge to the centroid.
• The sum of two convex components of is a polygon. This polygon is the affine image of a regular convex N-gon whose all vertices lie on an ellipse. (as pointed out by Nikhil)
• A necessary and sufficient condition for to have a convex midpoint polygon (after some finite iterations of the midpoint polygon procedure) is that the ellipse circumscribing the sum of two convex components of is nondegenerate. (The degenerate form of an ellipse is a point. )

For a nice outline of the proof, please refer to the comment by uncombed_coconut on previous post.

Since I didn’t know that this is a well studied problem (and that too by a well known mathematician!) I was trying to prove it on my own. Though I didn’t make much progress, but I discovered some interesting theorems which I will share in my future posts.

Midpoint Polygon Conjecture

This is going to be yet another ambitious post like New Diagonal Contribution Theorem, and Cross Diagonal Cover Problem.

Let’s begin with following definitions from Wikipedia:

A convex polygon is a simple polygon (not self-intersecting) in which no line segment between two points on the boundary ever goes outside the polygon.

A concave polygon is a simple polygon (not self-intersecting) which has at least one reflex interior angle – that is, an angle with a measure that is between 180 degrees and 360 degrees exclusive.

We know that 3 sided polygons (a.k.a triangles) are always convex.  So, they are not very interesting. Let’s define the following procedure:

Midpoint Polygon Procedure: Given a n-sided simple polygon, join the consecutive midpoints of the sides to generate another n-sided simple polygon.

Here are few examples:

Red polygon is the original polygon, green polygon is the one generated by joining midpoints.

We observe that if the original polygon was a concave polygon then the polygon generated by joining midpoints need not be a convex polygon. So, let’s try to observe what happens when we apply the midpoint polygon procedure iteratively on the 4th case above (i.e. when we didn’t get a convex polygon):

In fourth iteration of the described procedure, we get the convex polygon.

Based on this observation, I want to make following conjecture:

Midpoint Polygon Conjecture: For every simple polygon there exists a smallest natural number such that after iterations of midpoint polygon procedure, we obtain a convex polygon.

If the given polygon is convex, then there is nothing to prove since , but I have no idea about how to prove it for concave polygons. I tried to Google for the answer, but couldn’t find anything similar. So, if you know the proof or counterexample of this conjecture, please let me know.