In Madhava Mathematics Competition 2015 (held in January 2015), we were asked to prove the convergence of Kempner Series (first time proved in 1914). Recently I discovered the paper by A. J. Kempner (http://www.jstor.org/stable/2972074), so in this blog post I will state and prove that problem.
The basic idea behind proof is to divide whole series into chunks (finding symmetry) and then construct a converging geometric series which will act as upper bound of Kempner Seires.
Theorem (Kempner Series, 1914). Harmonic Series, , converge, if the denominators do not include all natural numbers
, converge, if the denominators do not include all natural numbers  , but only those numbers which do not contain any figure 9.
, but only those numbers which do not contain any figure 9.
Proof: Given Series is:

Now we can rewrite above series as:

where 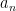 is the sum of all terms in
is the sum of all terms in  of denominator
of denominator  with
with 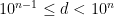 .
.
Observe that, each term of  which forms part of
which forms part of 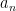 , is less than or equal to
, is less than or equal to  .
.
Now count the number of terms of  which are contained in
which are contained in 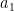 , in
, in 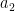 ,
,  , in
, in 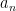 . Clearly,
. Clearly, 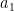 , consists of 8 terms, and
, consists of 8 terms, and 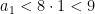 . In
. In 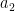 there are, as is easily seen, less than
there are, as is easily seen, less than  terms of
terms of  , and
, and  . Altogether there are in
. Altogether there are in  less than
less than 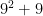 terms with denominators under 100.
terms with denominators under 100.
Assume now that we know the number of terms in  which are contained in
which are contained in 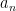 to be less than
to be less than  , for
, for  . Then, because each term of
. Then, because each term of  which is contained in
which is contained in 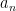 is not greater than
is not greater than  , we have
, we have 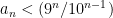 , and the total number of terms in
, and the total number of terms in  with denominators under
with denominators under  is less than
is less than  .
.
Now, let’s go for induction. For 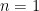 and
and 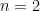 we have verified all this, and we will now show that if it is true for
we have verified all this, and we will now show that if it is true for  , then
, then  .
.  contains all terms in
contains all terms in  of denominator
of denominator  ,
, 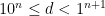 . This interval for
. This interval for  can be broken up into the nine intervals,
can be broken up into the nine intervals,  ,
, 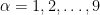 . The last interval does not contribute any term to
. The last interval does not contribute any term to  , the eight remaining intervals contribute each the same number of terms to
, the eight remaining intervals contribute each the same number of terms to  , and this is the same as the number of terms contributed by the whole interval
, and this is the same as the number of terms contributed by the whole interval  , that is, by assumption, less than
, that is, by assumption, less than  .
.
Therefore,  contains less than
contains less than  terms of
terms of  , and each of these terms is less than or equal to
, and each of these terms is less than or equal to  , we have
, we have  .
.
Hence, 
Thus,  converges, and since,
converges, and since,  ,
,  also converges.
also converges.
——————————–
Note: There is nothing special about 9 here, the above method of proof holds unchanged if, instead of 9, any other figure 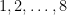 is excluded, but not for the figure
is excluded, but not for the figure 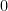 .
.

You must be logged in to post a comment.