Confusing terms in topology

Following are some of the terms used in topology which have similar definition or literal English meanings:

• Convex set: A subset of is called convex¹ , if it contains, along with any pair of its points , also the entire line segement joining the points.

• Star-convex set: A subset of is called star-convex if there exists a point such that for each , the line segment joining to lies in .

• Simply connected: A topological space is called simply connected if it is path-connected²  and any loop in defined by can be contracted³  to a point.

• Deformation retract: Let be a subspace of . We say  is a deformation retracts to if there exists a retraction⁴ a retraction such that its composition with the inclusion is homotopic⁵  to the identity map on .

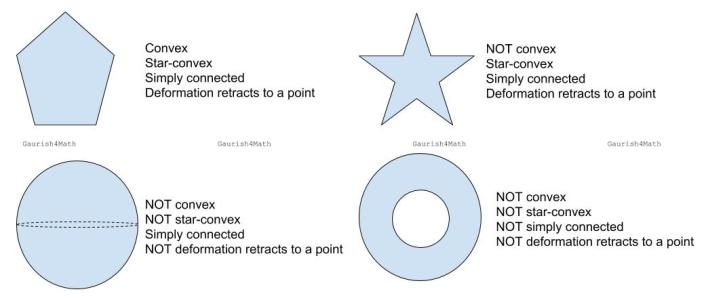
Various examples to illustrate the interdependence of these terms. Shown here are pentagon, star, sphere, and annulus.

A stronger version of Jordan Curve Theorem, known as Jordan–Schoenflies theorem, implies that the interior of a simple polygon is always a simply-connected subset of the Euclidean plane. This statement becomes false in higher dimensions.

The n-dimensional sphere is simply connected if and only if . Every star-convex subset of is simply connected. A torus, the (elliptic) cylinder, the Möbius strip, the projective plane and the Klein bottle are NOT simply connected.

The boundary of the n-dimensional ball , that is, the -sphere, is not a retract of the ball. Using this we can prove the Brouwer fixed-point theorem. However, deformation retracts to a sphere . Hence, though the sphere shown above doesn’t deformation retract to a point, it is a deformation retraction of .

---

Footnotes

1. In general, a convex set is defined for vector spaces. It’s the set of elements from the vector space such that all the points on the straight line line between any two points of the set are also contained in the set. If and are points in the vector space, the points on the straight line between and are given by for all from 0 to 1.
2. A path from a point to a point in a topological space is a continuous function from the unit interval to with and . The space is said to be path-connected if there is a path joining any two points in .
3. There exists a continuous map such that restricted to is . Here, and denotes the unit circle and closed unit disk in the Euclidean plane respectively. In general, a space is contractible if it has the homotopy-type of a point. Intuitively, two spaces and are homotopy equivalent if they can be transformed into one another by bending, shrinking and expanding operations.
4. Then a continuous map is a retraction if the restriction of to is the identity map on .
5. A homotopy between two continuous functions and from a topological space to a topological space is defined to be a continuous function such that, if then and . Deformation retraction is a special type of homotopy equivalence, i.e. a deformation retraction is a mapping which captures the idea of continuously shrinking a space into a subspace.

Advertisements

Hyperreal and Surreal Numbers

These are the two lesser known number systems, with confusing names.

Hyperreal numbers originated from what we now call “non-standard analysis”. The system of hyperreal numbers is a way of treating infinite and infinitesimal quantities. The term “hyper-real” was introduced by Edwin Hewitt in 1948. In non-standard analysis the concept of continuity and differentiation is defined using infinitesimals, instead of the epsilon-delta methods. In 1960, Abraham Robinson showed that infinitesimals are precise, clear, and meaningful.

source: https://math.stackexchange.com/a/51460/214604

Following is a relevant Numberphile video:

Surreal numbers, on the other hand, is a fully developed number system which is more powerful than our real number system. They share many properties with the real numbers, including the usual arithmetic operations (addition, subtraction, multiplication, and division); as such, they also form an ordered field. The modern definition and construction of surreal numbers was given by John Horton Conway in  1970. The inspiration for these numbers came from the combinatorial game theory. Conway’s construction was introduced in Donald Knuth‘s 1974 book Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness.

In his book, which takes the form of a dialogue, Knuth coined the term surreal numbers for what Conway had called simply numbers. This is the best source to learn about their construction. But the construction, though logical, is non-trivial. Conway later adopted Knuth’s term, and used surreals for analyzing games in his 1976 book On Numbers and Games.

Following is a relevant Numberphile video:

Many nice videos on similar topics can be found on PBS Infinite Series YouTube channel.

Number Theory

I read the term “number theory” for the first time in 2010, in this book (for RMO preparation):

This term didn’t make any sense to me then. More confusing was the entry in footer “Number of Theory”. At that time I didn’t have much access to internet to clarify the term, hence never read this chapter. I still like the term “arithmetic” rather than “number theory” (though both mean the same).

Yesterday, following article in newspaper caught my attention:

article: HT – How a Congress-BSP pact can be a game changer in MP, Rajasthan, Chhattisgarh

The usage of this term makes sense here!

Number Devil

If you enjoyed reading Lewis Carroll’s Alice’s Adventures in Wonderland, George Gamow’s Mr Tompkins, Abbott’s Flatland, Malba Tahan’s The Man Who Counted, Imre Lakatos’s Proofs and Refutations or Tarasov’s Calculus, then you will enjoy reading Enzensberger’s The Number Devil. But that is not an if and only if statement.

Originally written in German and published as Der Zahlenteufel, so far it has been translated into 26 languages (as per the back cover).

After reading this book one will have some knowledge of infinity, infinitesimal, zero, decimal number system, prime numbers (sieve of eratothenes, Bertrand’s postulate, Goldbach conjecture), rational numbers (0.999… = 1.0, fractions with 7 in denominator), irrational numbers (√2 = 1.4142…, uncountable), triangular numbers, square numbers, Fibonacci numbers, Pascal’s triangle (glimpse of Sierpinski triangle in it), combinatorics (permutations and combinations, role of Pascal’s triangle), cardinality of sets (countable sets like even numbers, prime numbers,…), infinite series (geometric series, harmonic series), golden ratio (recursive relations, continued fractions..), Euler characteristic (polyhedra and planar graphs), how to prove (11111111111^2 does not give numerical palindrome, Principia Mathematica), travelling salesman problem, Klein bottle, types of infinities (Cantor’s work), Euler product formula, imaginary numbers (Gaussian integer), Pythagoras theorem, lack of women mathematicians  and pi.

Since this is a translation of original work into English, you might not be happy with the language.  Though the author is not a mathematician, he is a well-known and respected European intellectual and author with wide-ranging interests. He gave a speech on mathematics and culture, “Zugbrücke außer Betrieb, oder die Mathematik im Jenseits der Kultur—eine Außenansicht” (“Drawbridge out of order, or mathematics outside of culture—a view from the outside”), in the program for the general public at  the International Congress of Mathematicians in Berlin in 1998. The speech was published under the joint sponsorship of the American Mathematical Society and the Deutsche Mathematiker Vereinigung as a pamphlet in German with facing English translation under the title Drawbridge Up: Mathematics—A Cultural Anathema, with an introduction by David Mumford.

Education System

This blog post has nothing to do with mathematics but just wanted to vent out my emotions.

I know that my opinions regarding the education system don’t matter since there always have been smarter people (i.e. people scoring more than me) around me in my home, school and college (and according to this system, only the opinions of top scorers matter). But, since WordPress allows me to express my opinions, here are the few comics which are in sync with my opinions:

© Bill Watterson

couldn’t find the creator of this comic

© Awantha Artigala

© Bill Watterson

I don’t think there is any solution to this problem since there are so many human beings on earth (i.e large variety of minds…).

A topic I wanted to discuss for long time

If you are an average maths undergraduate student (like me), you might have ended up in a situation of choosing between “just completing the degree by somehow passing the courses without caring about the grades” and “repeating a course/taking fewer courses so as to pass all courses with nice grades only”. Following is a nice discussion from Reddit:

Is it okay to take less credits? from learnmath

Understanding Geometry – 4

Aleksej Ivanovič Markuševič’s book, “Remarkable Curves” discusses the properties of ellipses, parabolas, hyperbolas, lemniscates, cycloids, brachistochrone, spirals and catenaries.  Among these “lemniscates” are the ones that I encountered only once before starting undergraduate education (all other curves appeared frequently in physics textbooks) and that too just to calculate the area enclosed by this curve. So I will discuss the properties of lemniscates in this post.

Let’s begin with the well-known curve, ellipse. An ellipse is the locus of points whose sum of distances from two fixed points (called foci) is constant. My favourite fact about ellipses is that we can’t find a general formula for the perimeter of an ellipse, and this little fact leads to the magical world of elliptic integrals. This, in turn, leads to the mysterious elliptic functions, which were discovered as inverse functions of elliptic integrals. Further, these functions are needed in the parameterization of certain curves, now called elliptic curves. For more details about this story, read the paper by Adrian Rice and Ezra Brown, “Why Ellipses are not Elliptic curves“.

Lemniscate is defined as the locus of points whose product of distances from two fixed points and (called foci) is constant. Lemniscate means, “with hanging ribbons” in Latin.  If the length of the segment is then for the midpoint of this line segment will lie on the curve if the product constant is . In this case we get a figure-eight lying on its side.

Lemniscate of Bernoulli; By Kmhkmh (Own work) [CC BY 4.0], via Wikimedia Commons

The attempt to calculate the perimeter of the above curve leads to elliptic integral, hence can’t derive a general formula for its perimeter. Just like an ellipse!

If we equate the value of the constant product not to but to another value, the lemniscate will change its shape. When the constant is less than , the lemniscate consists of two ovals, one of which contains inside it the point , and the other the point .

Cassini oval (x^2+y^2)^2−2c^2(x^2−y^2)=a^4−c^4; Source: https://www.encyclopediaofmath.org/legacyimages/common_img/c020700b.gif

When the product constant is greater than but less than , the lemniscate has the form of a biscuit. If the constant is close to , the “waist” of the biscuit is very narrow and the shape of the curve is very close to the figure-eight shape.

Cassini oval (x^2+y^2)^2−2c^2(x^2−y^2)=a^4−c^4; Source: https://www.encyclopediaofmath.org/legacyimages/common_img/c020700b.gif

If the constant differs little from , the waist is hardly noticeable, and if the constant is equal or greater than the waist disappears completely, and the lemniscate takes the form of an oval.

Cassini oval (x^2+y^2)^2−2c^2(x^2−y^2)=a^4−c^4; Source: https://www.encyclopediaofmath.org/legacyimages/common_img/c020700a.gif

We can further generalize this whole argument to get lemniscate with an arbitrary number of foci, called polynomial lemniscate.