Monthly Archives: May 2017

May28

Combinatorial Puzzle

Posted on by
Standard

This is a continuation of previous post:

How many distinct numbers can be formed by using four 2s and the four arithmetic operations +,-,\times, \div.

For example:
1 = \frac{2+2}{2+2}=\frac{2}{2}\times\frac{2}{2}
2 = 2+\frac{2-2}{2}=\frac{2}{2}+\frac{2}{2}
3 = 2+2 - \frac{2}{2}
4 = 2+2+2-2 = (2\times 2) + (2-2)
(note that some binary operations do not make sense without parenthesis)

I have no idea about how to approach this problem (since I am not very comfortable with combinatorics). So any help will be appreciated.

Edit[29 May 2017]: This problem has been solved in the comments below. 

May18

Arithmetic Puzzle

Posted on by
Standard

Following is a very common arithmetic puzzle that you may have encountered as a child:

Express any whole number n using the number 2 precisely four times and using only well-known mathematical symbols.

This puzzle has been discussed on pp. 172 of Graham Farmelo’s “The Strangest Man“, and how Paul Dirac solved it by using his knowledge of “well-known mathematical symbols”:

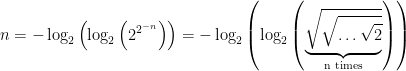
\displaystyle{n = -\log_{2}\left(\log_{2}\left(2^{2^{-n}}\right)\right) = -\log_{2}\left(\log_{2}\left(\underbrace{\sqrt{\sqrt{\ldots\sqrt{2}}}}_\text{n times}\right)\right)}

This is an example of thinking out of the box, enabling you to write any number using only three/four 2s. Though, using a transcendental function to solve an elementary problem may appear like an overkill.  But, building upon such ideas we can try to tackle the general problem, like the “four fours puzzle“.

This post on Puzzling.SE describes usage of following formula consisting of  trigonometric operation \cos(\arctan(x)) = \frac{1}{\sqrt{1+x^2}} and \tan(\arcsin(x))=\frac{x}{\sqrt{1-x^2}} to obtain the square root of any rational number from 0:

\displaystyle{\tan\left(\arcsin\left(\cos\left(\arctan\left(\cos\left(\arctan\left(\sqrt{n}\right)\right)\right)\right)\right)\right)=\sqrt{n+1}}.

Using this we can write n using two 2s:

\displaystyle{n = (\underbrace{\tan\arcsin\cos\arctan\cos\arctan}_{n-4\text{ times}}\,2)^2}

or even with only one 2:

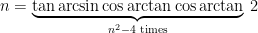
\displaystyle{n = \underbrace{\tan\arcsin\cos\arctan\cos\arctan}_{n^2-4\text{ times}}\,2}

May13

Intra-mathematical Dependencies

Posted on by
Standard

Recently I completed all of my undergraduate level maths courses, so wanted to sum up my understanding of mathematics in the following dependency diagram:

mat-dependency (1)

I imagine this like a wall, where each topic is a brick. You can bake different bricks at different times (i.e. follow your curriculum to learn these topics), but finally, this is how they should be arranged (in my opinion) to get the best possible understanding of mathematics.

As of now, I have an “elementary” knowledge of Set Theory, Algebra, Analysis, Topology, Geometry, Probability Theory, Combinatorics and Arithmetic. Unfortunately, in India, there are no undergraduate level courses in Mathematical Logic and Category Theory.

This post can be seen as a sequel of my “Mathematical Relations” post.

May7

Understanding Geometry – 3

Posted on by
Standard

In some of my past posts, I have mentioned “hyperbolic curvature“,”hyperbolic trigonometry” and “hyperbolic ideal points“. In this post I will share some artworks, based on hyperbolic geometry, by contemporary artists (from Tumblr):

https://www.tumblr.com/regolo54/88984180082

https://www.tumblr.com/regolo54/153466126772/hyperbolic

https://www.tumblr.com/regolo54/160221039662/hyperbolic

https://www.tumblr.com/regolo54/160327605897/hyperbolic

https://www.tumblr.com/adampizurny/160298780745/protobacillus-collab-with-adampizurny

To explain the mathematics behind the construction of these pictures I will quote Roger Penrose from pp. 34 of  “The Road to Reality“:

Think of any circle in a Euclidean plane. The set of points lying in the interior of this circle is to represent the set of points in the entire hyperbolic plane. Straight lines, according to the hyperbolic geometry are to be represented as segments of Euclidean circles which meet the bounding circle orthogonally — which means at right angles. Now, it turns out that the hyperbolic notion of an angle between any two curves, at their point of intersection, is precisely the same as the Euclidean measure of the angle between the two curves at the intersection point. A representation of this nature is called conformal. For this reason, the particular representation of hyperbolic geometry that Escher used is sometimes referred to as the conformal model of hyperbolic plane.

In the above-quoted paragraph, Penrose refers to Escher’s “Circle Limit” works, explained in detail by Bill Casselman in this article.