Number Theory

I read the term “number theory” for the first time in 2010, in this book (for RMO preparation):

This term didn’t make any sense to me then. More confusing was the entry in footer “Number of Theory”. At that time I didn’t have much access to internet to clarify the term, hence never read this chapter. I still like the term “arithmetic” rather than “number theory” (though both mean the same).

Yesterday, following article in newspaper caught my attention:

article: HT – How a Congress-BSP pact can be a game changer in MP, Rajasthan, Chhattisgarh

The usage of this term makes sense here!

Rooms and reflections

Consider the following entry from my notebook (16-Feb-2014):

The Art Gallery Problem: An art gallery has the shape of a simple n-gon. Find the minimum number of watchmen needed to survey the building, no matter how complicated its shape. [Source: problem 25, chapter 2, Problem Solving Strategies, Arthur Engel]

Hint: Use triangulation and colouring. Not an easy problem, and in fact there is a book dedicated to the theme of this problem: Art Gallery Theorems and Algorithms by Joseph O’Rourke (see chapter one for detailed solution). No reflection involved.

Then we have a bit harder problem when we allow reflection (28-Feb-2017, Numberphile – Prof. Howard Masur):

The Illumination Problem: Can any room (need not be a polygon) with mirrored walls be always illuminated by a single point light source, allowing for the repeated reflection of light off the mirrored walls?

The answer is NO. Next obvious question is “What kind of dark regions are possible?”. This question has been answered for rational polygons.

This reminds me of the much simpler theorem from my notebook (13-Jan-2014):

The Carpets Theorem: Suppose that the floor of a room is completely covered by a collection of non-overlapping carpets. If we move one of the carpets, then the overlapping area is equal to the uncovered area of the floor. [Source: §2.6, Mathematical Olympiad Treasures, Titu Andreescu & Bogdan Enescu]

Why I mentioned this theorem? The animation of Numberphile video reminded me of carpets covering the floor.

And following is the problem which motivated me write this blog post (17-May-2018, PBS Infinite Series – Tai-Danae):

Secure Polygon Problem: Consider a n-gon with mirrored walls, with two points: a source point S and a target point T. If it is possible to place a third point B in the polygon such that any ray from the source S passes through this point B before hitting the target T, then the polygon is said to be secure. Is square a secure polygon?

The answer is YES.  Moreover, the solution is amazing. Reminding me of the cross diagonal cover problem.

Evolution of Language

We know that statistics (which is different from mathematics) plays an important role in various other sciences (mathematics is not a science, it’s an art). But still I would like to discuss one very interesting application to linguistics. Consider the following two excerpts from an article by Bob Holmes:

1. ….The researchers were able to mathematically predict the likely “mutation rate” for each word, based on its frequency. The most frequently used words, they predict, are likely to remain stable for over 10,000 years, making these cultural artifacts, or “memes”, more stable than some genes…..

2. ….The most frequently used verbs (such as “be”, “have”, “come”, “go” and “take”) remained irregular. The less often a verb is used, the more likely it was to have been regularised. Of the rarest verbs in their list, including “bide”, “delve”, “hew”, “snip” and “wreak”, 91% have regularised over the past 1200 years…….

The first paragraph refers to  the work done by evolutionary biologist Mark Pagel and his colleagues at the University of Reading, UK. Also, “mathematically predicted” refers to the results of the statistical model analysing the frequency of use of words used to express 200 different meanings in 87 different languages. They found the more frequently the meaning is used in speech, the less change in the words used to express it.

The second paragraph refers to the work done by Erez Lieberman, Jean-Baptiste Michel and others at Harvard University, USA.  All people in this group have mathematical training.

I found this article interesting since I never expected biologists and mathematicians spending time on understanding evolution of language and publishing the findings in Nature journal. But this reminds me of the frequency analysis technique used in cryptanalysis:

Source: Enigma Cryptanalysis, Gaurish Korpal

Allostery

Cosider the folowing definiton:

Allostery is the process by which biological macromolecules (mostly proteins) transmit the effect of binding at one site to another, often distal, functional site, allowing for regulation of activity.

Many allosteric effects can be explained by the concerted MWC model put forth by Monod, Wyman, and Changeux, or by the sequential model described by Koshland, Nemethy, and Filmer.  The concerted model of allostery, also referred to as the symmetry model or MWC model, postulates that enzyme subunits are connected in such a way that a conformational change in one subunit is necessarily conferred to all other subunits. Thus, all subunits must exist in the same conformation. The model further holds that, in the absence of any ligand (substrate or otherwise), the equilibrium favors one of the conformational states, T (tensed) or R (relaxed). The equilibrium can be shifted to the R or T state through the binding of one ligand (the allosteric effector or ligand) to a site that is different from the active site (the allosteric site). [Wikipedia]

In this post, I want to draw attention towards application of mathematics in understanding biological process, allostery. Consider the following equation which relates the difference between , the number of binding sites, and , the Hill coefficient, to the ratio of the ligand binding function, 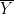, for oligomers with and ligand binding sites

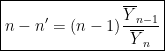
This is known as Crick-Wyman Equation  in enzymology, where and ; 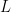is allosteric constant and is the concentration of ligand under some normalizaton conditions.

For derivation, see this article by Frédéric Poitevin and Stuart J. Edelstein. Also, you can read about history of this equation here.

It’s not uncommon to find simple differential equations in biochemistry (like Michaelis-Menten kinetics), but the above equation stated above is not a kinetics equation but rather a mathematical model for a biological phenomina. Comparable to the Hardy-Weinberg Equation discussed earlier.