These are the two lesser known number systems, with confusing names.
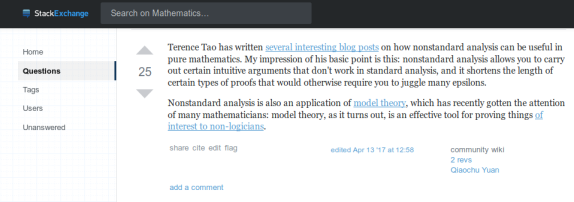
Hyperreal numbers originated from what we now call “non-standard analysis”. The system of hyperreal numbers is a way of treating infinite and infinitesimal quantities. The term “hyper-real” was introduced by Edwin Hewitt in 1948. In non-standard analysis the concept of continuity and differentiation is defined using infinitesimals, instead of the epsilon-delta methods. In 1960, Abraham Robinson showed that infinitesimals are precise, clear, and meaningful.
Following is a relevant Numberphile video:
Surreal numbers, on the other hand, is a fully developed number system which is more powerful than our real number system. They share many properties with the real numbers, including the usual arithmetic operations (addition, subtraction, multiplication, and division); as such, they also form an ordered field. The modern definition and construction of surreal numbers was given by John Horton Conway in 1970. The inspiration for these numbers came from the combinatorial game theory. Conway’s construction was introduced in Donald Knuth‘s 1974 book Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness.

In his book, which takes the form of a dialogue, Knuth coined the term surreal numbers for what Conway had called simply numbers. This is the best source to learn about their construction. But the construction, though logical, is non-trivial. Conway later adopted Knuth’s term, and used surreals for analyzing games in his 1976 book On Numbers and Games.
Following is a relevant Numberphile video:
Many nice videos on similar topics can be found on PBS Infinite Series YouTube channel.
You must be logged in to post a comment.