Monthly Archives: December 2015

Dec25

Maze

Posted on December 25, 2015 by math

Solving mazes is a great time-pass, if you “too” have nothing to do just try to solve this maze made by me (very easy one, can be solved within few seconds)

Very easy example of maze

Since I am writing about mazes, there must be something mathematical about them. Indeed “solving a maze” is a NP-complete problem [Non-deterministic Polynomial-time solvable problem], one of most popular class of problems in Theoretical Computer Science. But, no surprise here, since lot of puzzles like Minesweeper, sudoku etc. too are NP-complete.

Leonhard Euler was one of the first to analyze plane mazes mathematically, and in doing so made the first significant contributions to the branch of mathematics known as topology.

Mazes containing no loops are known as “standard”, or “perfect” mazes, and are equivalent to a tree in graph theory. Thus many maze solving algorithms are closely related to graph theory. Intuitively, if one pulled and stretched out the paths in the maze in the proper way, the result could be made to resemble a tree (dead ends become the leaves of the tree.).

To make my maze I used “adding walls algorithm” i.e. I laid a set of obstructions within an open area. Can you tell whether my maze above is “perfect” one??

As it turns out, there are various maze generation as well as maze solving algorithms. A detailed discussion of these can be found at: http://www.astrolog.org/labyrnth/algrithm.htm

Also, there is an interesting article on Maze solving using image analysis: http://www.crisluengo.net/index.php/archives/277

Dec22

Happy Birthday Ramanujam

Posted on December 22, 2015 by math

Standard

Today is 128th birthday of Srinivasa Ramanujam Iyengar.

[Please note that Britishers gave wrong English spelling for his name, they called him “Ramanujan”, but it should be “Ramanujam” which means “The younger brother of Lord Rama”]

John Littlewood said (as recalled by G. H. Hardy (1921), in “Obituary Notices: Srinivasa Ramanujan”, Proceedings of the London Mathematical Society 19, p. lvii) :

Every positive integer is one of Ramanujan’s personal friends.

So, let’s talk about numbers on his birthday.

128 is 7th power of 2 and leads to 4th Mersenne Prime ( $2^7 - 1=127$ is a prime)

128 is the largest number which is not the sum of distinct squares. [https://oeis.org/A001422]

and here is my present for him:

RAMANUJAM’S MAGIC SQUARE

When I was in High School, I learned making such “Special Date Magic Squares” form P.K. Srinivasan’s (1924-2005) book regarding Ramanujam’s work. [see: https://nrich.maths.org/1380 ]

Magic sum of this square is 69. Thus all rows, columns and diagonals add up to the same total of 69 and today’s date has been placed in first row.

69 is a value of $n$ where $n^2$ and $n^3$ together contain each digit once. Since, $69^2=4761$ and $69^3 = 328509$

[ http://www2.stetson.edu/~efriedma/numbers.html]

Ramanujam also studied “Partition Function”, this function gives the number of ways of writing the integer n as a sum of positive integers, where the order of addends is not considered significant. Observe that, in the magic square above we created 10 distinct 4-partitions of 69. (though 2376 distinct 4-partitions of 69 are possible!!)

Also, the total sum of numbers in our magic square is $69\cdot 4 = 276 = 1^5 + 2^5 + 3^5$

Once more, Happy Birthday Ramanujam!

Dec18

How NOT to teach mathematics

Posted on December 18, 2015 by math

Standard

When will people learn “how to teach mathematics?”

For example, Vigyan Prasar (Department of Science & Technology, Govt. of India) telecasts a 13 part video serial: गणित की सीढियां (The Maths Factor), on Lok Sabha TV Every Saturday at 11.00-11.30 am from 05 December, 2015.

Source: http://www.vigyanprasar.gov.in/whats_new/tv-programme-on-air.htm

Episode synopsis of the episode titled “The Calculus Enigma” reads:

This episode explores the ever so scary concept within mathematics- Calculus!

I just now came to know that “calculus is a scary concept of mathematics”.

Also, episode synopsis of the episode titled “Topology” gives a brand new WRONG definition for Topology:

Topology is the study of unusual shapes.

Another, episode synopsis of the episode titled “Number Sense” reads:

Anywhere in the world – China, Arabia, Africa, Venezuela – languages, font, metaphors change – but the number systems are truly universal.

The author of above episode should seriously read Wikipedia article: Numeral system. Are Roman and Hindu-Arabic number system same?

I really feel pity for people who make such filthy episodes.

Also, National Council of Educational Research and Training (Ministry of Human Resource Development, Govt. of India), publishes Mathematics textbooks for class 1 to 12 (in हिन्दी , اردو and English). And, interestingly at starting of Chapter -1 of Class XII Mathematics Textbook, G. H. Hardy has been quoted:

There is no permanent place in the world for ugly mathematics … . It may be very hard to define mathematical beauty but that is just as true of beauty of any kind, we may not know quite what we mean by a beautiful poem, but that does not prevent us from recognizing one when we read it.

Ironically, no public library in India has books by G. H. Hardy!

Dec15

Solution : Free cab ride

Posted on December 15, 2015 by math

Standard

It has been one month since I posted the puzzle. But since nobody solved it, here is my solution.

Let’s consider examples:

Number of people	Number of free rides
1	0
2	2
3	4
4	6

I can illustrate above counting with simple figure:

Each line segment represent two free rides for the group, since every time you refer someone, both referee and new customer get free ride.

From above observations we can conclude by Principle of Mathematical Induction, (try yourself!):

A group of $n$ people can enjoy at most $2(n-1)$ rides.

Dec7

Beauty Beyond Language

Posted on December 7, 2015 by math

Standard

Mathematics is believed to be a language of symbols with metamathematical meaning attached to them, for example:

$(\forall \varepsilon>0) (\exists N \in \mathbb{N}) \ni m,n \geq N \Rightarrow |a_m - a_n| < \varepsilon$

Can be translated in English as:

For every positive real number, $\varepsilon$ , there exists a natural number, $N$ , such that, if the natural numbers $m$ and $n$ are greater than or equal to $N$ then absolute value of the difference between $a_m$ and $a_n$ is less than $\varepsilon$

Many contemporary mathematicians (big-shots) like Jean-Pierre Serre , believe that instead of logographic language (symbols represent the words themselves), we should use alphabetic language (words are made up of various letters) . This also makes sense to me, because as seen in above example, symbols seem to hide beautiful simplicity of a mathematical statement. But, on the other hand, alphabetic language is too lengthy to write.

Because of above debates about language of Mathematics, many mathematicians love Proof without Words, consider an example by Mariano Suárez-Alvarez (http://mathoverflow.net/q/8847):

$1+2+\ldots + (n-1) = \frac{n(n-1)}{2}=\binom{n}{2}$

But, there are some sub-domains in mathematics which doesn’t depend on language, for example Geometry. Let me illustrate this point with following Spanish video created by Cristóbal Vila (Instituto Universitario de Matemáticas y Aplicaciones of the Universidad de Zaragoza):

Irrespective of the language you speak, you can appreciate the relationship between different artistic works and mathematics (mainly, Geometry)

For full details of this project see: http://www.etereaestudios.com/docs_html/arsqubica_htm/

Dec3

So many Integrals – II

Posted on December 3, 2015 by math

Standard

As promised in previous post, now I will briefly discuss the remaining two flavors of Integrals.

Stieltjes Integral

Stieltjes

In 1894, a Dutch mathematician, Thomas Stieltjes, while solving the moment problem, that is, given the moments of all orders of a body, find the distribution of its mass, gave a generalization of the Darboux integral.

Let $P : a = x_0 < x_1 < x_2<\ldots < x_n = b$ , $n$ being an integer, be a partition of the interval $[a, b]$ .

For a function $\alpha$ , monotonically increasing on $[a,b]$ , we write:

$\Delta \alpha_i = \alpha(x_i) - \alpha(x_{i-1})$

Let $f$ be a bounded function defined on an interval $[a, b],\quad a, b$ being real numbers. We define the sum

$S_P = \sum_{i=1}^n f(t_i)\Delta \alpha_i, \quad \overline{S}_P = \sum_{i=1}^n f(s_i)\Delta \alpha_i$

where $t_i,s_i \in [x_{i-1} , x_i]$ be such that

$f(t_i) = \text{sup} \{ f(x) : x \in [x_{i-1}, x_{i}]\}$ ,

$f(s_i) = \text{inf} \{ f(x) : x \in [x_{i-1}, x_{i}]\}$

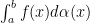If the $\text{inf}\{S_P\}$ and $\text{sup}\{\overline{S}_P\}$ are equal, we denote the common value by $\int_{a}^{b} f(x) d\alpha(x)$ and call it Steiltjes integral of $f$ with respect to $\alpha$ over $[a,b]$ .

Lebesgue Integral

Lebesgue

Let me quote Wikipedia article:

The integral of a function f between limits a and b can be interpreted as the area under the graph of f. This is easy to understand for familiar functions such as polynomials, but what does it mean for more exotic functions? In general, for which class of functions does “area under the curve” make sense? The answer to this question has great theoretical and practical importance.

In 1901, a French mathematician, Henri Léon Lebesgue generalized the notion of the integral by extending the concept of the area below a curve to include functions with uncountable discontinuities .

Lebesgue defined his integral by partitioning the range of a function and summing up sets of x-coordinates belonging to given y-coordinates, rather than, as had traditionally been done, partitioning the domain.

Lebesgue himself, according to his colleague, Paul Montel, compared his method with paying off a debt: (see:pp. 803, The Princeton Companion to Mathematics)

I have to pay a certain sum, which I have collected in my pocket. I take the bills and coins out of my pocket and give them to the creditor in the order I find them until I have reached the total sum. This is the Riemann integral. But I can proceed differently. After I have taken all the money out of my pocket I order the bills and coins according to identical values and then I pay the several heaps one after the other to the creditor. This is my integral.

A set 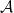$\mathcal{A}$ is said to be Lebesgue measurable, if for each set 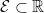$\mathcal{E} \subset \mathbb{R}$ the Carathéodory condition:

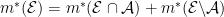
$m^{*} (\mathcal{E}) = m^{*}(\mathcal{E} \cap \mathcal{A}) + m^{*}(\mathcal{E}\backslash \mathcal{A})$

is satisfied, where $m^{*}(\mathcal{A})$ is called outer measure and is defined as:

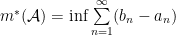
$m^{*}(\mathcal{A}) = \inf\sum\limits_{n=1}^\infty (b_n-a_n)$

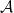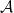where $\mathcal{A}$ is a countable collection of closed intervals $[a_n,b_n], a_n\leq b_n$ , that cover $\mathcal{A}$ .

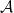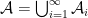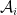The Lebesgue integral of a simple function $\phi(x) = \sum_{i=1}^n c_i \chi_{\mathcal{A}_i} (x)$ on $\mathcal{A}$ , where $\mathcal{A}=\bigcup_{i=1}^{\infty} \mathcal{A}_{i}$ , $\mathcal{A}_i$ are pairwise disjoint measurable sets and $c_1, c_2, \ldots$ are real numbers, is defined as:

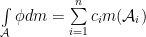
$\int\limits_{\mathcal{A}} \phi dm = \sum\limits_{i=1}^{n} c_i m(\mathcal{A}_i)$

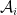where, $m(\mathcal{A}_i)$ is the Lebesgue measure of a measurable set $\mathcal{A}_i$ .

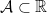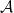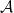An extended real value function $f: \mathcal{A}\rightarrow \overline{\mathbb{R}}$ defined on a measurable set $\mathcal{A}\subset\mathbb{R}$ is said to be Lebesgue measurable on $\mathcal{A}$ if $f^{-1} ((c,\infty]) = \{x \in\mathcal{A} : f(x) > c\}$ is a Lebesgue measurable subset of $\mathcal{A}$ for every real number $c$ .

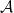If $f$ is Lebesgue measurable and non-negative on $\mathcal{A}$ we define:

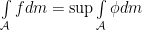
$\int\limits_{\mathcal{A}} f dm = \sup \int\limits_{\mathcal{A}} \phi dm$

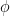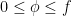where the supremum is taken over all simple functions $\phi$ such that $0\leq \phi \leq f$ .

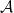The function $f$ is said to be Lebesgue integrable on $\mathcal{A}$ if it’s integral over 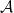$\mathcal{A}$ is finite.

The Lebesgue integral is deficient in one respect. The Riemann integral generalizes to the improper Riemann integral to measure functions whose domain of definition is not a closed interval. The Lebesgue integral integrates many of these functions, but not all of them.

Gaurish4Math

For the love of Mathematics

Monthly Archives: December 2015

Maze

Happy Birthday Ramanujam

How NOT to teach mathematics

Solution : Free cab ride

Beauty Beyond Language

So many Integrals – II