You would have heard about imaginary numbers and most famous of them is 
. I personally don’t like this name because all of mathematics is man/woman made, hence all mathematical objects are imaginary (there is no perfect circle in nature…) and lack physical meaning. Moreover, these numbers are very useful in physics (a.k.a. the study of nature using mathematics). For example, “time-dependent Schrödinger equation”
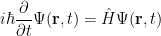
But, as described here:
Complex numbers are a tool for describing a theory, not a property of the theory itself. Which is to say that they can not be the fundamental difference between classical and quantum mechanics (QM). The real origin of the difference is the non-commutative nature of measurement in QM. Now this is a property that can be captured by all kinds of beasts — even real-valued matrices. [Physics.SE]
For more of such interpretation see: Volume 1, Chapter 22 of “The Feynman Lectures in Physics”. And also this discussion about Hawking’s wave function.
All these facts may not have fascinated you, but the following fact from Einstein’s Special Relativity should fascinate you:
In 1908 Hermann Minkowski explained how the Lorentz transformation could be seen as simply a hyperbolic rotation of the spacetime coordinates, i.e., a rotation through an imaginary angle. [Wiki: Rapidity]
Irrespective of the fact that you do/don’t understand Einstein’s relativity, the concept of imaginary angle appears bizarre. But, mathematically its just another consequence of non-euclidean geometry which can be interpreted as Hyperbolic law of cosines etc. For example:
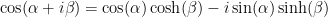
Let’s try to understand what is meant by “imaginary angle” by following the article “A geometric view of complex trigonometric functions” by Richard Hammack. Consider the complex unit circle 
of 
, in a manner exactly analogous to the definition of the standard unit circle in 
. Apparently U is some sort of surface in , but it can’t be drawn as simply as the usual unit circle, owing to the four-dimensional character of 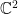. But we can examine its lower dimensional cross sections. For example, if 
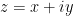and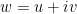 
then by setting 
we get the circle 
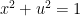in x-u plane for v=0 and the hyperbola 
in x-vi plane for u=0.
The cross-section of complex unit circle (defined by z^2+w^2=1 for complex numbers z and w) with the x-u-vi coordinate space (where z=x+iy and w=u+iv) © 2007 Mathematical Association of America
These two curves (circle and hyperbola) touch at the points ±o, where o=(1,0) in 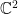, as illustrated above. The symbol o is used by Richard Hammack because this point will turn out to be the origin of complex radian measure.
Let’s define complex distance between points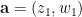 
and 
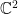in as
where square root is the half-plane H of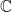 
consisting of the non-negative imaginary axis and the numbers with a positive real part. Therefore, the complex distance between two points in 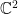is a complex number (with non-negative real part).
Starting at the point o in the figure above, one can move either along the circle or along the right-hand branch of the hyperbola. On investigating these two choices, we conclude that they involve traversing either a real or an imaginary distance. Generalizing the idea of real radian measure, we define imaginary radian measure to be the oriented arclength from o to a point p on the hyperbola, as
(a) Real radian measure (b) Imaginary radian measure. © 2007 Mathematical Association of America
If p is above the x axis, its radian measure is 
with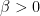 
, while if it is below the x axis, its radian measure is with 
. As in the real case, we define 
and 
to be the z and w coordinates of p. According to above figure (b), this gives
Notice that both these relations hold for both positive and negative values of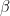 
, and are in agreement with the expansions of 
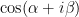and 
stated earlier.
But, to “see” what a complex angle looks like we will have to examine the complex versions of lines and rays. Despite the four dimensional flavour, 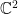is a two-dimensional vector space over the field 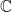, just like over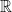 
.
Since a line (through the origin) in is the span of a nonzero vector, we define a complex line in 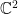analogously. For a nonzero vector u in 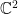, the complex line 
through u is span(u), which is isomorphic to the complex plane.
In , the ray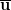 
passing through a nonzero vector u can be defined as the set of all nonnegative real multiples of u. Extending this to 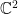seems problematic, for the word “nonnegative” has no meaning in 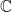. Using the half-plane H (where complex square root is defined) seems a reasonable alternative. If u is a nonzero vector in , then the complex ray through u is the set 
.
Finally, we define a complex angle is the union of two complex rays 
and 
.
I will end my post by quoting an application of imaginary angles in optics from here:
… in optics, when a light ray hits a surface such as glass, Snell’s law tells you the angle of the refracted beam, Fresnel’s equations tell you the amplitudes of reflected and transmitted waves at an interface in terms of that angle. If the incidence angle is very oblique when travelling from glass into air, there will be no refracted beam: the phenomenon is called total internal reflection. However, if you try to solve for the angle using Snell’s law, you will get an imaginary angle. Plugging this into the Fresnel equations gives you the 100% reflectance observed in practice, along with an exponentially decaying “beam” that travels a slight distance into the air. This is called the evanescent wave and is important for various applications in optics. [Mathematics.SE]
Gaurish4Math 
You must be logged in to post a comment.