A couple of weeks ago I discussed a geometric solution to an arithmetic problem. In this post, I will discuss an arithmetical solution to a geometry problem. Consider the following question:
Given a square whose sides are reflecting mirrors. A ray of light leaves a point inside the square and is reflected repeatedly in the mirrors. What is the nature of its paths?
It may happen that the ray passes through a corner of the square. In that case, we assume that it returns along its former path.

In figure, the parallels to the axis are the lines,  and
and  , where
, where  and
and  are integers. The thick square, of side 1, around the origin is the square of the problem and
are integers. The thick square, of side 1, around the origin is the square of the problem and  is the starting point. We construct all images of
is the starting point. We construct all images of  in the mirrors, for direct or repeated reflection. One can observe that they are of four types, the coordinates of the images of the different types being
in the mirrors, for direct or repeated reflection. One can observe that they are of four types, the coordinates of the images of the different types being

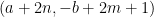


where  and
and  are arbitrary integers. Further, if the velocity at
are arbitrary integers. Further, if the velocity at  has direction cosines,
has direction cosines,  , then the corresponding images of the velocity have direction cosines
, then the corresponding images of the velocity have direction cosines



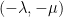
where we suppose (on the grounds of symmetry) that  is positive. If we think of the plane as divided into squares of unit side, then interior of a typical square being
is positive. If we think of the plane as divided into squares of unit side, then interior of a typical square being
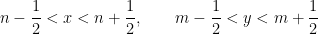
then each squares contains just one image of every point in the original sqaure, given by  (shown by the bold points in the figure). And if the image in any of the above squares of any point in the original sqaure is of type (1.), (2.), (3.) or (4.), then the image in any of the above squares of any other point in the original square is of the same type.
(shown by the bold points in the figure). And if the image in any of the above squares of any point in the original sqaure is of type (1.), (2.), (3.) or (4.), then the image in any of the above squares of any other point in the original square is of the same type.
We can now imagine  moving with the ray (shown by dotted lines in the figure). When the point
moving with the ray (shown by dotted lines in the figure). When the point  meets the mirror, it coincides with an image and the image of
meets the mirror, it coincides with an image and the image of  which momentarily coincides with
which momentarily coincides with  continues the motion of
continues the motion of  , in its original direction, in one of the squares adjacent to the fundamental square (the thick square). We follow the motion of the image, in this square, until it in its turn it meets a side of the square. Clearly, the original path of
, in its original direction, in one of the squares adjacent to the fundamental square (the thick square). We follow the motion of the image, in this square, until it in its turn it meets a side of the square. Clearly, the original path of  will be continued indefinitely in the same line
will be continued indefinitely in the same line 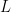 (dotted line in the figure), by a series of different images.
(dotted line in the figure), by a series of different images.
The segment of 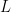 in any square (for a given
in any square (for a given  and
and  ) is the image of a straight portion of the path of
) is the image of a straight portion of the path of  in the original square. There is one-to-one correspondence between the segments of
in the original square. There is one-to-one correspondence between the segments of 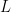 , in different squares, and the portions of the path of
, in different squares, and the portions of the path of  between successive reflections, each segment of
between successive reflections, each segment of 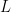 being an image of the corresponding portion of the path of
being an image of the corresponding portion of the path of  .
.
The path of  in the original square will be periodic if
in the original square will be periodic if  returns to its original position moving in the same direction; and this will happen if and only if
returns to its original position moving in the same direction; and this will happen if and only if 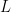 passes through an image of type (1.) of the original
passes through an image of type (1.) of the original  . The coordinates of an arbitrary point of
. The coordinates of an arbitrary point of 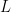 are
are  .
.
Hence the path will be periodic if and only if  , for some
, for some 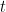 and integral
and integral  , i.e. if
, i.e. if 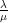 is rational.
is rational.
When 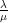 is irrational, then the path of
is irrational, then the path of  approaches arbitrarily near to every point
approaches arbitrarily near to every point 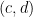 of the sqaure. This follows directly from Kronecker’s Theorem in one dimension (see § 23.3 of G H. Hardy and E. M. Wright’s An Introduction to the Theory of Numbers.):
of the sqaure. This follows directly from Kronecker’s Theorem in one dimension (see § 23.3 of G H. Hardy and E. M. Wright’s An Introduction to the Theory of Numbers.):
[Kronecker’s Theorem in one dimension] If  is irrational,
is irrational,  is arbitrary, and
is arbitrary, and  and
and  are positive, then there are integers
are positive, then there are integers  and
and 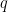 such that
such that  and
and  .
.
Here, we have 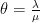 and
and  , with large enough integers
, with large enough integers 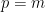 and
and  . Hence we can conclude that
. Hence we can conclude that
[König-Szücs Theorem]Given a square whose sides are reflecting mirrors. A ray of light leaves a point inside the square and is reflected repeatedly in the mirrors. Either the path is closed and periodic or it is dense in the square, passing arbitrarily near to every point of the square. A necessary and sufficient condition for the periodicity is that the angle between a side of the square and the initial direction of the ray should have a rational tangent.
Another way of stating the above Kronecker’s theorem is
[Kronecker’s Theorem in one dimension] If  is irrational, then the set of points
is irrational, then the set of points  is dense in the interval
is dense in the interval 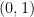 .
.
Then with some knowledge of Fourier series, we can try to answer a more general question
Given an irrational number  , what can be said about the distribution of the fractional parts of the sequence of numbers
, what can be said about the distribution of the fractional parts of the sequence of numbers  , for
, for 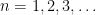 ?
?
The answer to this question is called Weyl’s Equidistribution Theorem (see §4.2 of Elias M. Stein & Rami Shakarchi’s Fourier Analysis: An Introduction)
[Weyl’s Equidistribution Theorem] If  is irrational, then the sequence of fractional parts
is irrational, then the sequence of fractional parts 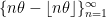 is equidistributed in
is equidistributed in  .
.
I really enjoyed reading about this unexpected link between geometry and arithmetic (and Fourier analysis). Most of the material has been taken/copied from Hardy’s book. The solution to the geometry problem reminds me of the solution to the Cross Diagonal Cover Problem.
for which
is an integer. Clearly, if
then
is an integer. So let’s consider the case when
where
and
. Substituting this value of
we get:
we conclude that
. Also it’s clear that
. Hence,
and we just need to find the possible values of
.
we get:
. Since
, we have
, that is,
.
we get
. Hence we conclude that the non-integer values of
which lead to integer output are:
for all








You must be logged in to post a comment.