Tag Archives: rational numbers

Jun15

Rational input, integer output

Posted on by
Standard

Consider the following polynomial equation [source: Berkeley Problems in Mathematics, problem 6.13.10]:

f(t) = 3t^3 + 10t^2 - 3t

Let’s try to figure out the rational values of t for which f(t) is an integer. Clearly, if t\in\mathbb{Z} then f(t) is an integer. So let’s consider the case when t=m/n where \gcd(m,n)=1 and m\neq \pm 1. Substituting this value of t we get:

\displaystyle{f\left(\frac{m}{n}\right) = \frac{3m^3}{n^3} + \frac{10m^2}{n^2} - \frac{3m}{n}= \frac{m(3m^2+10mn-3n^2)}{n^3}=k \in \mathbb{Z}}

Since, n^3\mid (3m^2+10mn-3n^2) we conclude that n\mid 3. Also it’s clear that m\mid k. Hence, n=\pm 3 and we just need to find the possible values of m.

For n=3 we get:

\displaystyle{f\left(\frac{m}{3}\right) =  \frac{m(m^2+10m-9)}{9}=k \in \mathbb{Z}}

Hence we have 9\mid (m^2+10m). Since \gcd(m,n)=\gcd(m,3)=1, we have 9\mid (m+10), that is, m\equiv 8\pmod 9.

Similarly, for m=-3 we get n\equiv 1 \pmod 9. Hence we conclude that the non-integer values of t which lead to integer output are:

\displaystyle{t = 3\ell+ \frac{8}{3}, -3\ell-\frac{1}{3}} for all \ell\in\mathbb{Z}

 

Aug25

Polynomials and Commutativity

Posted on by
Standard

In high school, I came to know about the statement of the fundamental theorem of algebra:

Every polynomial of degree n with integer coefficients have exactly n complex roots (with appropriate multiplicity).

In high school, a polynomial = a polynomial in one variable. Then last year I learned 3 different proofs of the following statement of the fundamental theorem of algebra [involving, topology, complex analysis and Galois theory]:

Every non-zero, single-variable, degree n polynomial with complex coefficients has, counted with multiplicity, exactly n complex roots.

A more general statement about the number of roots of a polynomial in one variable is the Factor Theorem:

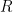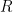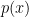Let R be a commutative ring with identity and let p(x)\in R[x] be a polynomial with coefficients in R. The element a\in R is a root of p(x) if and only if (x-a) divides p(x).

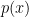A corollary of above theorem is that:

A polynomial f of degree n over a field F has at most n roots in F.

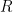(In case you know undergraduate level algebra, recall that R[x] is a Principal Ideal Domain if and only if R is a field.)

The key fact that many times go unnoticed regarding the number of roots of a given polynomial (in one variable) is that the coefficients/solutions belong to a commutative ring (and 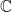\mathbb{C} is a field hence a commutative ring). The key step in the proof of all above theorems is the fact that the division algorithm holds only in some special commutative rings (like fields). I would like to illustrate my point with the following fact:

The equation X^2 + X + 1 has only 2 complex roots, namely \omega = \frac{-1+i\sqrt{3}}{2} and \omega^2 = \frac{-1-i\sqrt{3}}{2}. But if we want solutions over 2×2 matrices (non-commutative set) then we have at least  3 solutions (consider 1 as 2×2 identity matrix and 0 as the 2×2 zero matrix.)

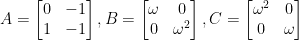
\displaystyle{A=\begin{bmatrix} 0 & -1 \\1 & -1 \end{bmatrix}, B=\begin{bmatrix} \omega & 0 \\0 & \omega^2 \end{bmatrix}, C=\begin{bmatrix} \omega^2 & 0 \\0 & \omega \end{bmatrix}}

if we allow complex entries. This phenominona can also be illusttrated using a non-commutative number system, like quaternions. For more details refer to this Math.SE discussion.

Apr23

Huntington’s Red-Blue Set

Posted on by
Standard

While reading Lillian Lieber’s book on infinity, I came across an astonishing example of infinite set (on pp. 207). Let’s call the property of existence of a rational number between given two rational number to be “beauty” (a random word introduced by me to make arguments clearer).

The set of rational numbers between 0 and 1 are arranged in ascending order of magnitude, and all of them are coloured blue. This is clearly a beautiful set. Then another another set of rational numbers between 0 and 1 is taken and arrange in ascending order of magnitude, but all of them are coloured red. This is also a beautiful set. Now, put these two sets together in such a way that each blue number is immediately followed by the corresponding red number. For example, 1/2 is immediately followed by 1/2 etc.  It appears that if we interlace two beautiful sets, the resulting set should be even more beautiful. But since each blue number has an immediate successor, namely the corresponding red number, so that between these two we can’t find even a single other rational number, red or blue, the resulting set is NOT beautiful.

The set created above is called Huntington’s Red-Blue set. It is an ingenious invention, where two beautiful sets combined together lead to loss of beauty. For more details, read the original paper:

Huntington, Edward V. “The Continuum as A Type of Order: An Exposition of the Modern Theory.” Annals of Mathematics, Second Series, 7, no. 1 (1905): 15-43. doi:10.2307/1967192.

Feb1

Rationals…

Posted on by
Standard

A few days ago I noticed some fascinating properties of so called rational numbers.

Natural Bias:

Our definition of a number being rational or irrational is very much biased. We implicitly assume our numbers to be in decimals (base 10), and then define rational numbers as those numbers which have terminating or recurring decimal representation.

But it is interesting to note that, for example, √5 is irrational in base-10 (non-terminating, non-repeating decimal representation) but if we consider “golden-ratio base“, √5 = 10.1, has terminated representation, just like rational number!!

Ability to complete themselves:

When we construct numbers following Peano’s Axioms we can “easily” create (set of) natural numbers (\mathbb{N}), and from them integers (\mathbb{Z}) and rational numbers (\mathbb{Q}). Notice that \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q}.

But it is comparatively difficult to create real numbers (\mathbb{R}) from rational numbers (\mathbb{Q}) although still we want to create a set from its subset. Notice that unlike previous cases, to create \mathbb{R} we will first have to create so-called irrational numbers (\overline{\mathbb{Q}}) from \mathbb{Q}. The challenge of creating the complementary set (\overline{\mathbb{Q}}) of a given set (\mathbb{Q}) using the given set (\mathbb{Q}) itself makes it difficult to create \mathbb{R} from \mathbb{Q} . We overcome this difficulty by using specialized techniques like Dedekind cut or Cauchy sequences (the process is called “completion of rational numbers”).