
We all know that, area is the basis of integration theory, just as counting is basis of the real number system. So, we can say:
An integral is a mathematical operator that can be interpreted as an area under curve.
But, in mathematics we have various flavors of integrals named after their discoverers. Since the topic is a bit long, I have divided it into two posts. In this and next post I will write their general form and then will briefly discuss them.
Cauchy Integral

Newton, Leibniz and Cauchy (left to right)
This was rigorous formulation of Newton’s & Leibniz’s idea of integration, in 1826 by French mathematician, Baron Augustin-Louis Cauchy.
Let  be a positive continuous function defined on an interval
be a positive continuous function defined on an interval ![[a, b],\quad a, b](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D%2C%5Cquad+a%2C+b&bg=ffffff&fg=000000&s=0&c=20201002) being real numbers. Let
being real numbers. Let  ,
,  being an integer, be a partition of the interval
being an integer, be a partition of the interval ![[a, b]](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D&bg=ffffff&fg=000000&s=0&c=20201002) and form the sum
and form the sum
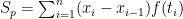
where ![t_i \in [x_{i-1} , x_i]f](https://s0.wp.com/latex.php?latex=t_i+%5Cin+%5Bx_%7Bi-1%7D+%2C+x_i%5Df&bg=ffffff&fg=000000&s=0&c=20201002) be such that
be such that ![f(t_i) = \text{Minimum} \{ f(x) : x \in [x_{i-1}, x_{i}]\}](https://s0.wp.com/latex.php?latex=f%28t_i%29+%3D+%5Ctext%7BMinimum%7D+%5C%7B+f%28x%29+%3A+x+%5Cin+%5Bx_%7Bi-1%7D%2C+x_%7Bi%7D%5D%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002)
By adding more points to the partition 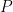 , we can get a new partition, say
, we can get a new partition, say  , which we call a ‘refinement’ of
, which we call a ‘refinement’ of  and then form the sum
and then form the sum  . It is trivial to see that
. It is trivial to see that 
Since,  is continuous (and positive), then
is continuous (and positive), then 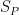 becomes closer and closer to a unique real number, say
becomes closer and closer to a unique real number, say  , as we take more and more refined partitions in such a way that
, as we take more and more refined partitions in such a way that 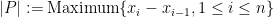 becomes closer to zero. Such a limit will be independent of the partitions. The number
becomes closer to zero. Such a limit will be independent of the partitions. The number  is the area bounded by function and x-axis and we call it the Cauchy integral of
is the area bounded by function and x-axis and we call it the Cauchy integral of  over
over  to
to 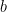 . Symbolically,
. Symbolically, 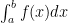 (read as “integral of f(x)dx from a to b”).
(read as “integral of f(x)dx from a to b”).
Riemann Integral

Riemann
Cauchy’s definition of integral can readily be extended to a bounded function with finitely many discontinuities. Thus, Cauchy integral does not require either the assumption of continuity or any analytical expression of  to prove that the sum
to prove that the sum  indeed converges to a unique real number.
indeed converges to a unique real number.
In 1851, a German mathematician, Georg Friedrich Bernhard Riemann gave a more general definition of integral.
Let ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0&c=20201002) be a closed interval in
be a closed interval in 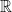 . A finite, ordered set of points
. A finite, ordered set of points  ,
,  being an integer, be a partition of the interval
being an integer, be a partition of the interval ![[a, b]](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Let,
. Let, 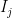 denote the interval
denote the interval ![[x_{j-1}, x_j], j= 1,2,3,\ldots , n](https://s0.wp.com/latex.php?latex=%5Bx_%7Bj-1%7D%2C+x_j%5D%2C+j%3D+1%2C2%2C3%2C%5Cldots+%2C+n&bg=ffffff&fg=000000&s=0&c=20201002) . The symbol
. The symbol  denotes the length of
denotes the length of 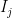 . The mesh of
. The mesh of 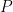 , denoted by
, denoted by 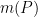 , is defined to be
, is defined to be 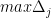 .
.
Now, let  be a function defined on interval
be a function defined on interval ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0&c=20201002) . If, for each
. If, for each 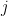 ,
,  is an element of
is an element of 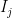 , then we define:
, then we define:

Further, we say that 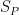 tend to a limit
tend to a limit  as
as 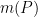 tends to 0 if, for any
tends to 0 if, for any 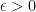 , there is a
, there is a 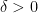 such that, if
such that, if 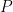 is any partition of
is any partition of ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0&c=20201002) with
with  , then
, then 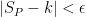 for every choice of
for every choice of  .
.
Now, if 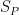 tends to a finite limit as
tends to a finite limit as 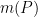 tends to zero, the value of the limit is called Riemann integral of
tends to zero, the value of the limit is called Riemann integral of  over
over ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0&c=20201002) and is denoted by
and is denoted by 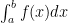
Darboux Integral

Darboux
In 1875, a French mathematician, Jean Gaston Darboux gave his way of looking at the Riemann integral, defining upper and lower sums and defining a function to be integrable if the difference between the upper and lower sums tends to zero as the mesh size gets smaller.
Let  be a bounded function defined on an interval
be a bounded function defined on an interval ![[a, b],\quad a, b](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D%2C%5Cquad+a%2C+b&bg=ffffff&fg=000000&s=0&c=20201002) being real numbers. Let
being real numbers. Let  ,
,  being an integer, be a partition of the interval
being an integer, be a partition of the interval ![[a, b]](https://s0.wp.com/latex.php?latex=%5Ba%2C+b%5D&bg=ffffff&fg=000000&s=0&c=20201002) and form the sum
and form the sum

where ![t_i,s_i \in [x_{i-1} , x_i]](https://s0.wp.com/latex.php?latex=t_i%2Cs_i+%5Cin+%5Bx_%7Bi-1%7D+%2C+x_i%5D&bg=ffffff&fg=000000&s=0&c=20201002) be such that
be such that
![f(t_i) = \text{sup} \{ f(x) : x \in [x_{i-1}, x_{i}]\}](https://s0.wp.com/latex.php?latex=f%28t_i%29+%3D+%5Ctext%7Bsup%7D+%5C%7B+f%28x%29+%3A+x+%5Cin+%5Bx_%7Bi-1%7D%2C+x_%7Bi%7D%5D%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002) ,
,
![f(s_i) = \text{inf} \{ f(x) : x \in [x_{i-1}, x_{i}]\}](https://s0.wp.com/latex.php?latex=f%28s_i%29+%3D+%5Ctext%7Binf%7D+%5C%7B+f%28x%29+%3A+x+%5Cin+%5Bx_%7Bi-1%7D%2C+x_%7Bi%7D%5D%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002)
The sums 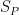 and
and 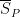 represent the areas and
represent the areas and  . Moreover, if
. Moreover, if 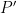 is a refinement of
is a refinement of 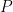 , then
, then

Using the boundedness of  , one can show that
, one can show that 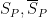 converge as the partition get’s finer and finer, that is
converge as the partition get’s finer and finer, that is  , to some real numbers, say
, to some real numbers, say  respectively. Then:
respectively. Then:

If  , then we have
, then we have  .
.
There are two more flavours of integrals which I will discuss in next post. (namely, Stieltjes Integral and Lebesgue Integral)
be a set of natural numbers such that
, and
are not prime numbers. Show that
is a composite number, we have
for some, not necessarily distinct, primes
and
. Next,
implies that
. Therefore we have:
, we desire to find the exact value of this sum. This is where it’s convinient to recognize that
. Since we know what are Bernoulli numbers, we can use the following formula for Riemann zeta-function:
, so for
we have
. Hence completing the proof
as done by Euler while solving the Basel problem (though at that time the notion of convergence itself was not well defined):






You must be logged in to post a comment.